A sphere is one of the most fascinating and fundamental geometric shapes that exist in both theoretical and practical contexts. From the celestial bodies in our universe to everyday objects like balls and marbles, spheres play an essential role in our lives. Understanding the properties and applications of spheres is crucial for various fields, including mathematics, physics, engineering, and design.
Spheres are three-dimensional objects that possess unique characteristics, such as symmetry and uniformity, making them indispensable in scientific studies and industrial applications. As we delve deeper into this article, we will explore the mathematical principles behind spheres, their real-world applications, and the significance they hold in our daily lives.
Whether you're a student, professional, or simply someone curious about the wonders of geometry, this comprehensive guide aims to provide you with valuable insights into the world of spheres. Let's embark on this journey of discovery together!
Read also:Matthew Gray Gubler Movies And Tv Shows A Comprehensive Guide
Table of Contents
- What is a Sphere?
- Key Properties of a Sphere
- Mathematical Formulas for Spheres
- Real-World Applications of Spheres
- Types of Spheres
- The Role of Spheres in Science
- Spheres in Engineering and Technology
- Historical Perspective of Spheres
- Challenges and Innovations in Sphere Design
- The Future of Spheres in Modern Technology
- Conclusion and Final Thoughts
What is a Sphere?
A sphere is a perfectly round three-dimensional object where all points on its surface are equidistant from its center. This geometric shape is defined by its radius, which is the distance from the center to any point on the surface. Unlike other three-dimensional shapes, such as cubes or pyramids, spheres exhibit uniform symmetry and lack any edges or vertices.
In mathematical terms, a sphere can be described using the equation:
(x - a)² + (y - b)² + (z - c)² = r²
Where (a, b, c) represents the coordinates of the center, and r is the radius of the sphere.
Spheres are found in nature and man-made objects alike, showcasing their versatility and importance in various domains. Their inherent properties make them ideal for numerous applications, ranging from scientific research to industrial design.
Key Properties of a Sphere
Uniformity and Symmetry
Spheres possess uniformity and symmetry, making them unique among three-dimensional shapes. Every cross-section of a sphere is a circle, and all diameters passing through the center are equal in length. This symmetry simplifies calculations and makes spheres highly desirable in fields requiring precision and balance.
Read also:Juan Gabriel Laura Salas A Legacy Of Love Music And Advocacy
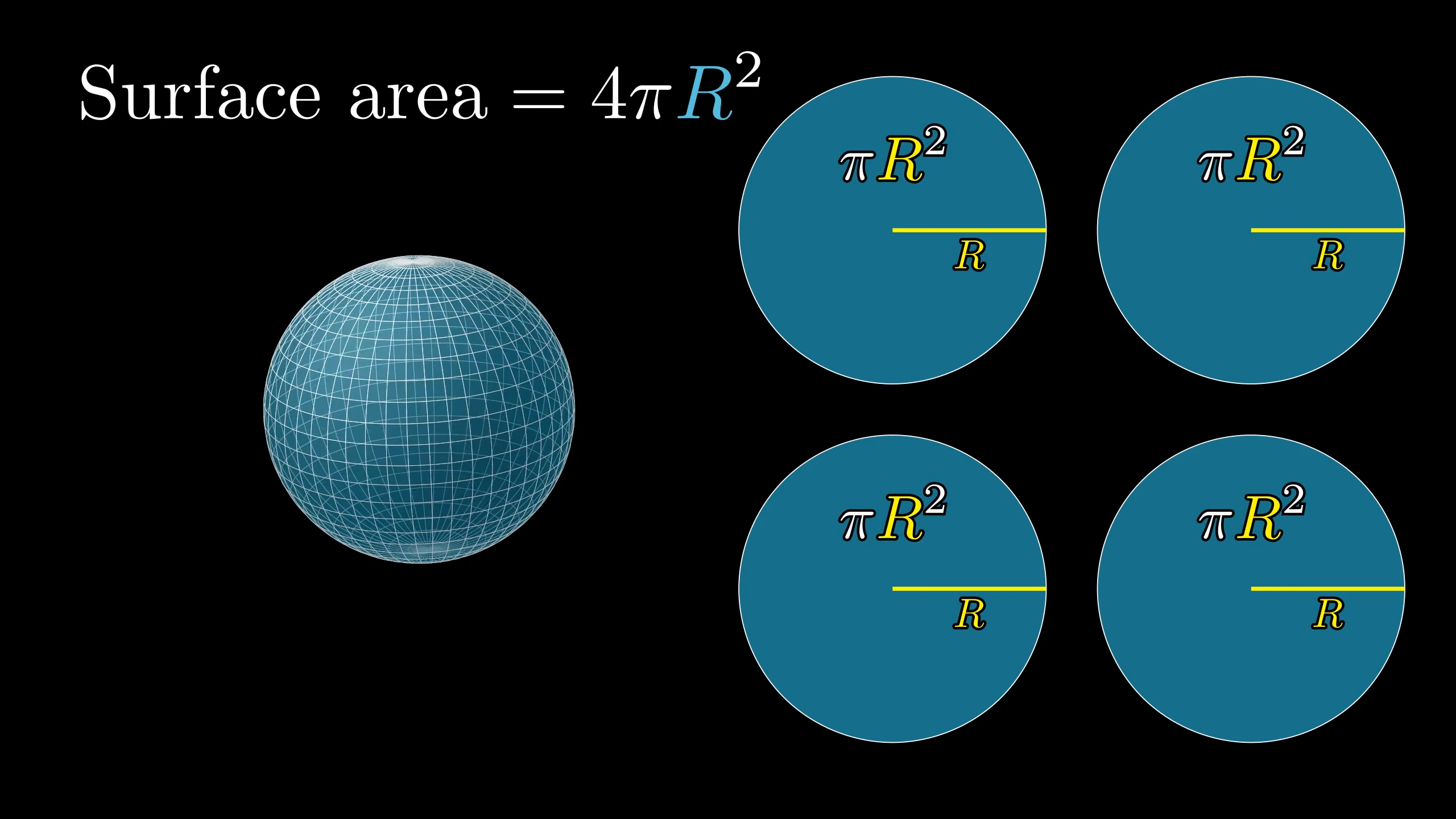
Surface Area and Volume
Two critical properties of spheres are their surface area and volume, which can be calculated using the following formulas:
- Surface Area = 4πr²
- Volume = (4/3)πr³
These formulas highlight the relationship between the radius and the physical dimensions of the sphere, enabling accurate measurements and predictions.
Optimal Packing Efficiency
Spheres are known for their optimal packing efficiency, especially in arrangements like hexagonal close packing and face-centered cubic packing. This property is crucial in industries such as logistics, where maximizing space utilization is paramount.
Mathematical Formulas for Spheres
Beyond surface area and volume, spheres have several other mathematical formulas associated with them. These include:
- Great Circle Distance: The shortest distance between two points on the surface of a sphere, calculated using spherical trigonometry.
- Spherical Coordinates: A coordinate system used to describe the position of points on a sphere, consisting of radial distance, polar angle, and azimuthal angle.
- Spherical Cap: The portion of a sphere cut off by a plane, with formulas for calculating its surface area and volume.
These formulas are essential for solving complex problems involving spheres in various disciplines.
Real-World Applications of Spheres
In Astronomy
Spheres are integral to astronomy, where celestial bodies such as planets, stars, and moons are often approximated as spheres due to their nearly uniform shapes. Understanding the geometry of spheres helps astronomers calculate distances, orbits, and other critical parameters.
In Sports
Many sports involve spherical objects, such as soccer balls, basketballs, and tennis balls. The design of these objects takes into account the aerodynamic properties of spheres to ensure optimal performance during play.
In Medicine
In medical imaging, spheres are used as reference objects for calibrating equipment and testing imaging algorithms. Additionally, spherical lenses are employed in eyeglasses and contact lenses to correct vision impairments.
Types of Spheres
Perfect Spheres
A perfect sphere is an idealized geometric shape where all points on its surface are equidistant from the center. While rare in nature, perfect spheres serve as a theoretical basis for many scientific and engineering applications.
Near-Spheres
Many objects in the real world approximate spheres but deviate slightly due to imperfections or external factors. Examples include planets, which are slightly oblate due to their rotation, and manufactured spheres with minor surface irregularities.
Hollow Spheres
Hollow spheres, such as bubbles or balloons, consist of a thin outer layer enclosing an empty interior. These objects exhibit unique physical properties, such as buoyancy and flexibility, making them valuable in various applications.
The Role of Spheres in Science
Spheres play a vital role in scientific research, providing insights into phenomena ranging from atomic structures to large-scale cosmic events. For instance:
- Atomic Models: Spheres are used to represent electrons orbiting around atomic nuclei in quantum mechanics.
- Gravitational Studies: Spherical objects are ideal for studying gravitational forces, as their symmetry simplifies calculations.
- Fluid Dynamics: Spheres are employed in experiments to analyze drag forces and flow patterns in fluids.
These applications demonstrate the versatility and importance of spheres in advancing scientific knowledge.
Spheres in Engineering and Technology
In engineering, spheres are utilized in various applications due to their strength, durability, and resistance to deformation. Some notable examples include:
- Bearing Balls: Spherical bearings are used in machinery to reduce friction and enable smooth motion.
- Pressure Vessels: Spherical tanks and containers are designed to withstand high pressures while minimizing material usage.
- Robotic Design: Spherical joints and components are incorporated into robots to achieve multi-axis movement and flexibility.
These innovations highlight the practical significance of spheres in modern engineering practices.
Historical Perspective of Spheres
The study of spheres dates back to ancient civilizations, where early mathematicians and philosophers explored their properties and applications. Notable figures such as Euclid and Archimedes made significant contributions to the understanding of spheres, laying the foundation for future developments.
Throughout history, spheres have been used in art, architecture, and navigation, showcasing their cultural and practical importance. From the spherical domes of ancient temples to the globes used for mapping the Earth, spheres have left an indelible mark on human history.
Challenges and Innovations in Sphere Design
Despite their simplicity, designing and manufacturing perfect spheres presents several challenges. Factors such as material limitations, manufacturing tolerances, and environmental conditions can affect the accuracy and performance of spherical objects.
Innovations in technology, such as advanced machining techniques and 3D printing, have enabled the creation of highly precise spheres for specialized applications. These advancements continue to push the boundaries of what is possible with spherical designs.
The Future of Spheres in Modern Technology
As technology continues to evolve, the role of spheres in various industries is expected to expand. Emerging fields such as nanotechnology, robotics, and space exploration are likely to benefit from the unique properties of spheres, leading to groundbreaking discoveries and innovations.
Additionally, the integration of artificial intelligence and machine learning in sphere-related applications promises to enhance their functionality and efficiency, paving the way for a new era of technological advancement.
Conclusion and Final Thoughts
In conclusion, spheres are remarkable geometric shapes with a wide range of applications in science, engineering, and everyday life. Their unique properties and versatility make them indispensable in various fields, driving progress and innovation.
We invite you to explore further by leaving your thoughts and questions in the comments section below. Additionally, feel free to share this article with others who may find it informative and engaging. For more insightful content, don't hesitate to browse our other articles on related topics.
Thank you for joining us on this journey to unravel the mysteries of spheres. Together, let's continue to expand our knowledge and appreciation of this fascinating subject!